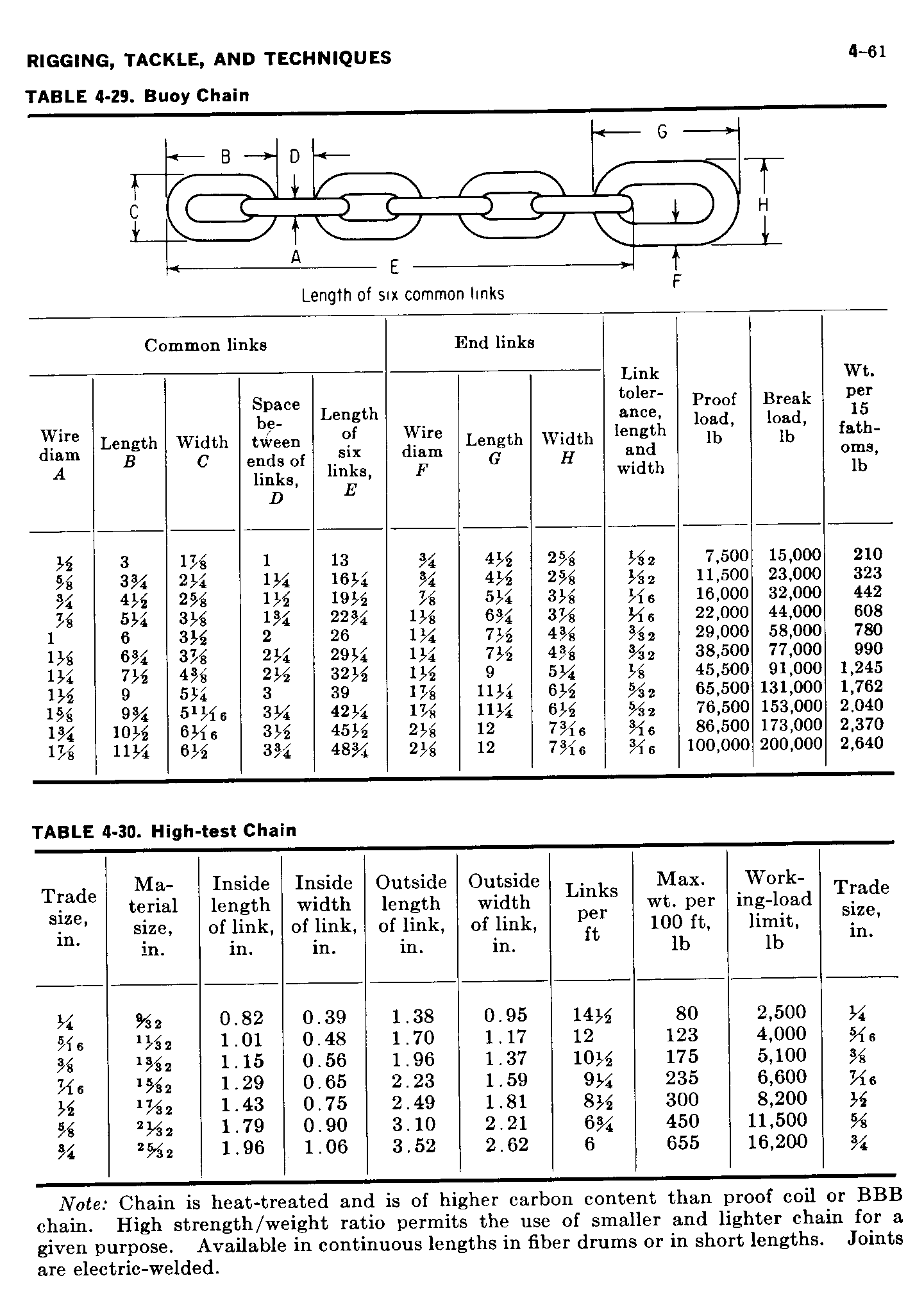
Buoy Chain
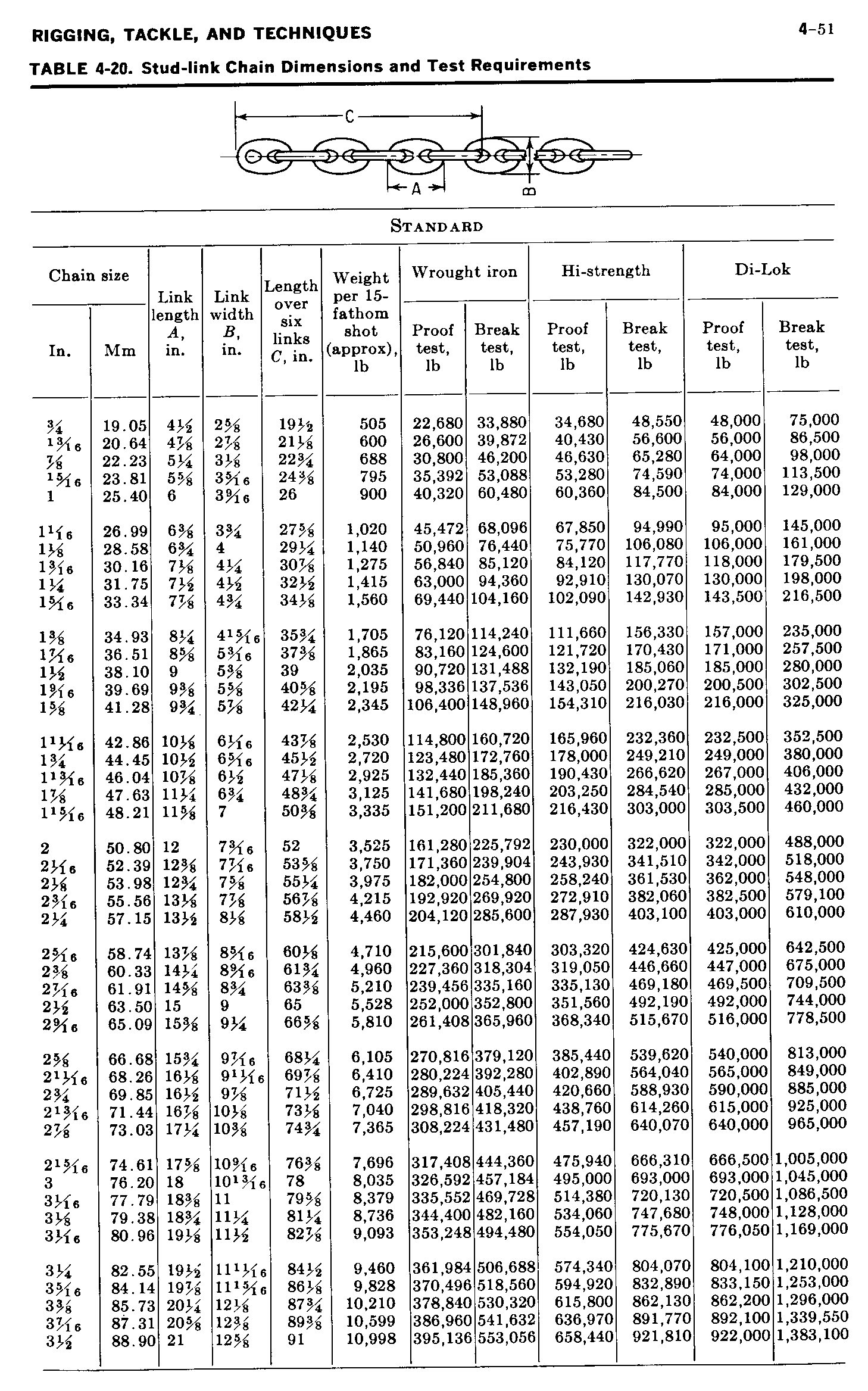
Stud-Link Chain
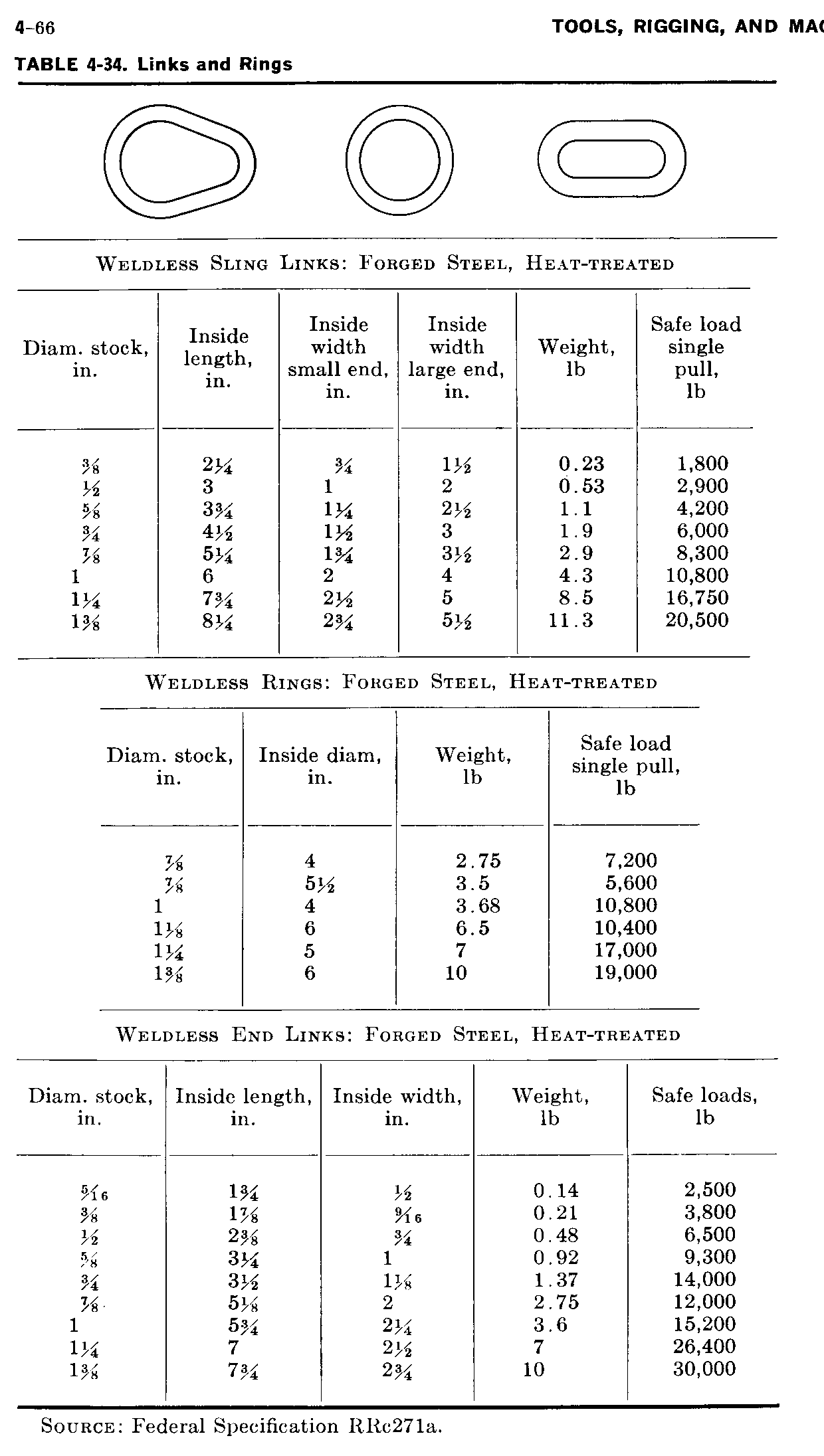
Links and Rings
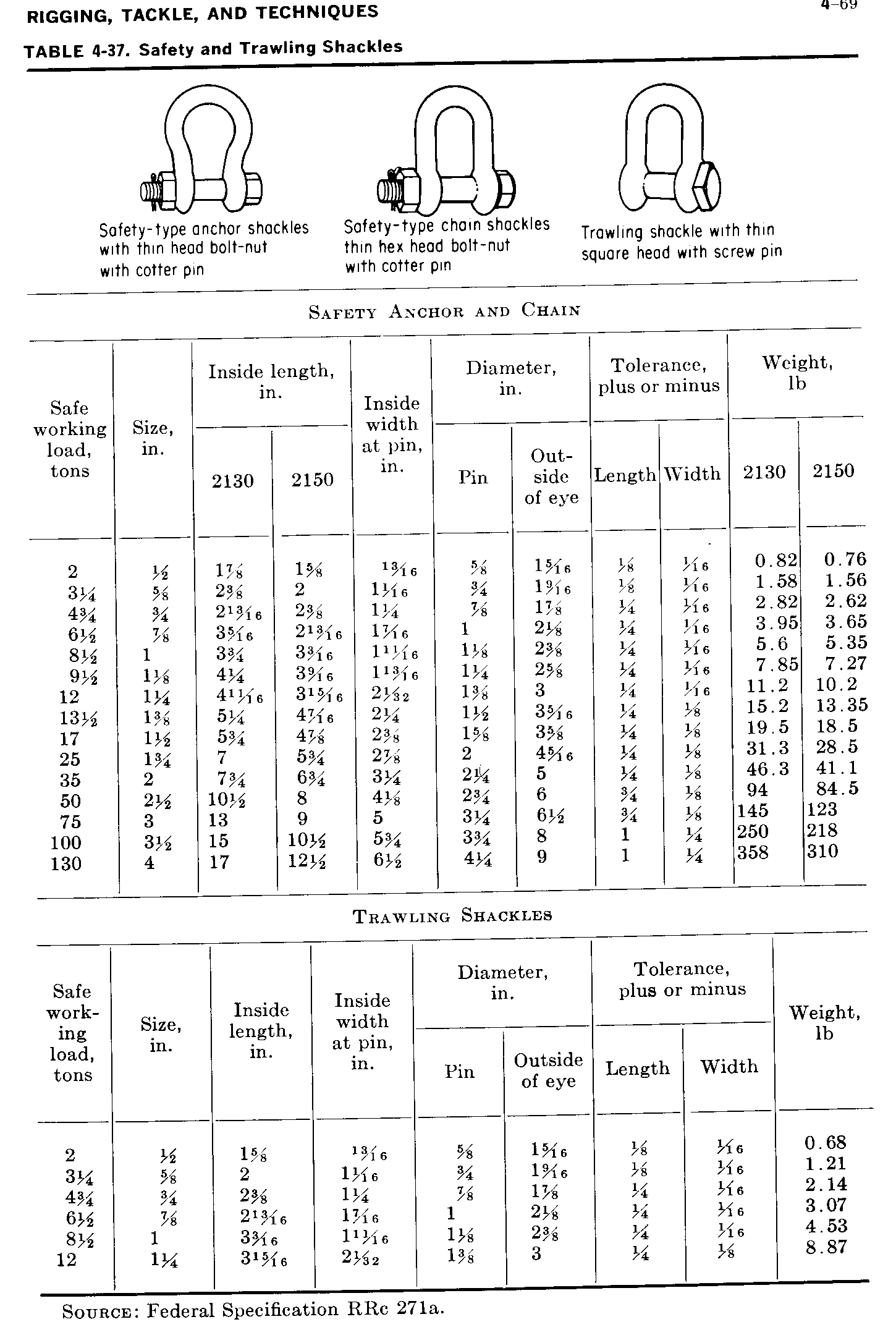
Safety and Nut Shackles
Screw Shackles
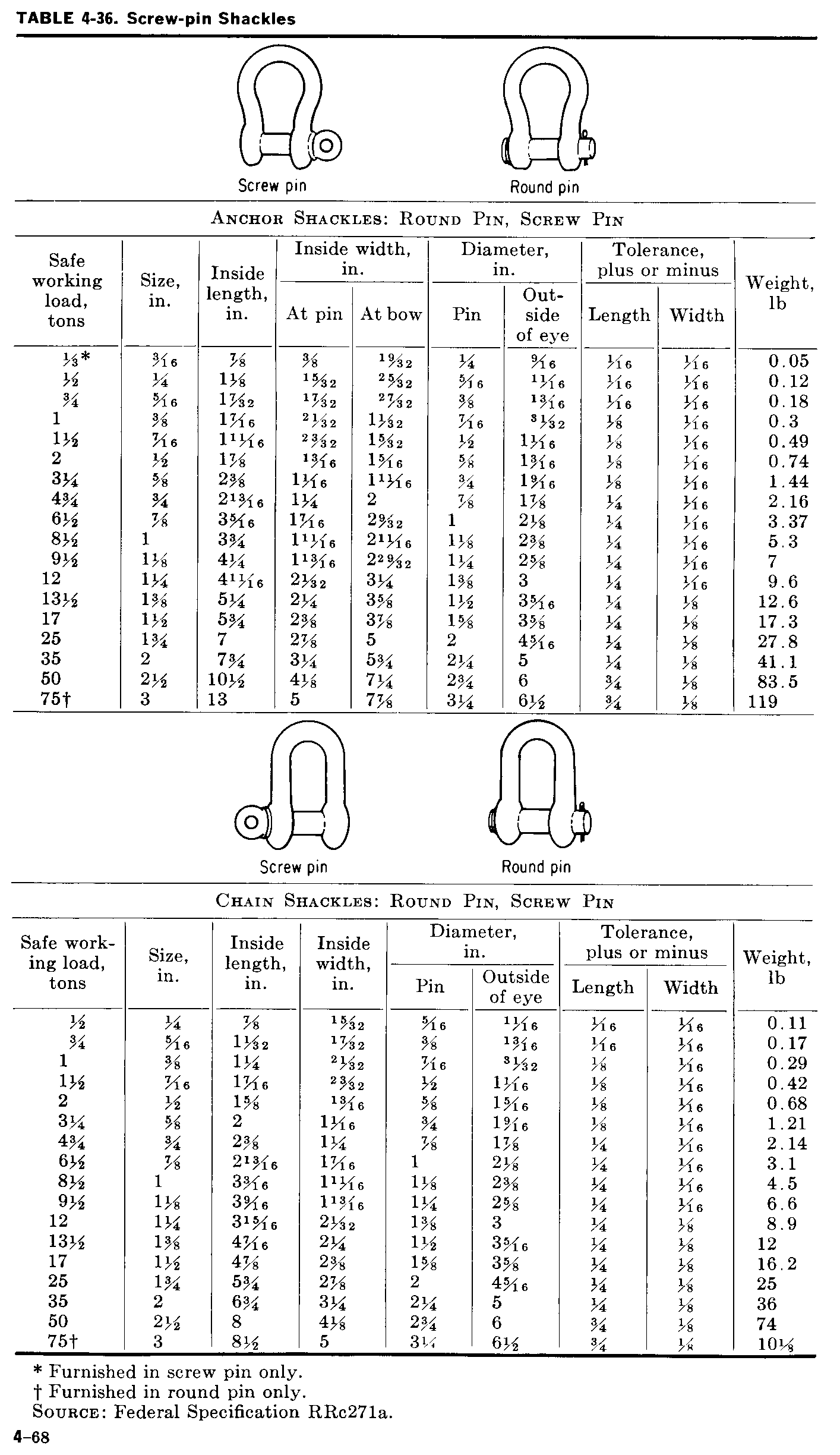
The following images where scanned from Myers, Holm and McAllister's Book "Handbook of Ocean and Underwater Engineering". They are reproduced here for the benefit of designing oceanographic moorings using the Mooring Design and Dynamics package for MATLAB. The information is provided to assist in determining the size, weight, and strength characteristics of various steel chains, shackles and joiners. I originally build MD&D in 1999, in the relatively early days of the Internet. There are now many sites with chain and mooring component specifications on the Web. Also, metric dimensions are now routinely listed either next to or replacing emperical dimensions. I strongly recommend that "rated' gear be used in all oceanographic moorings, such as "Crosby" (www.thecrosbygroup.com). I do not endorse any manufacturer nor hold any liability for mooring loss or harm due to broken gear. When in doubt, reported working loads should be more than twice the maximum loads you anticipate lifting.
The conversion from lb. (pounds) to kg is 1 kg = 2.2046 lb, and steel retains approximately 87% of it's weight (negative buoyancy) in seawater. Therefore a 20 lb length of chain weighs 20/2.2046=9.072 kg in air, and 9.072*0.87=7.91 kg in seawater. Since it is heavier than seawater, we would assign it a negative buoyancy of -7.91 kg. But also note all length components, such as wire, chain, rope etc. are all specified in MD&D by the weight per (unit) metre [kg/m]. Connectors (e.g. shackles) are unit weight.
Mooring Design and Dynamics wants mass/lengths of chain and wire to be entered as the buoyancy per unit meter of length. For example, in the table for buoy chain, the weights are given in pounds (lb) per 15 fathoms of length, which equals approximately 27.432 m (6ft = 1 fathom = 1.8288m). So for 1/2 inch buoy chain, with a weight of 210 lb per 15 fathoms, the buoyancy per unit metre is: -210[lb/fthm]/27.432[m/fthm] = -7.6553[lb/m] /2.2046[lb/kg] = -3.4724[kg/m] *0.87 = -3.021[kg/m], where steel retains about 87% (*0.87)of it's mass submerged in seawater.
Also note that the safe loads reported here are under a constant tension and do not represent "snap" loads. When a line goes slack, and elements may start to rise/fall/shift, they gain momentum. If tension is then allowed to "snap" back on, the forces involved must first overcome the impact (force x time) associated with stopping any motion (momentum), before the tension can take the raw "weight" again. This short period of a "snap-load" can introduce forces that are many times (even orders of magnitude) larger than static loads. Snap loads can occur, for example, when the surface float (or ship) is subject to wave action. A towed body, or anchor/mooring line may then experience a snap load, effectively equal to or greater than the weight of the object (many tons). It is snap-loads during mooring deployment or recovery from a ship in a sea state that will usually break a mooring line. The only rough way to estimate the potential forces [kg] of a snap-load is the in-air weight of the object subject to the motion. An example would be an anchor first mooring deployment, with the mooring hanging with it's anchor from the stern of a ship (e.g. through the A-frame) in, say, 2-3m seas. The line may go slack as the stern (A-frame) falls/descends, allowing the mooring line (with it's anchor) to free fall. Then the stern starts to rise on the next wave, and the mooring line comes back under tension, it must first stop (acount for any momentum) the descending mooring/anchor, before the mooring/anchor can rise with the ship/A-frame. This rapid turn-around introduces a snap-load that will be far in excess of the weight of the mooring/anchor, likely breaking the mooring line at it's weakest link (e.g. un-rated shackle). This has happened to me, and many other oceanographers. Not only will you loose mooring components, you may injure someone and will certainly not have the respect of any ship crew or officer. See for example the paper by Niedzwecki and Thampi (1991). So be very (extra) careful with any potential snap-load scenario.
Finally, the following gif images and this HTML document may NOT print well from browsers, in that the page breaks can/may not be controlled.
If you have any questions, please contact me at rkdewey@gmail.com




